1. 降低语法分析树高度

优化语法无法改变语法分析器的渐进行为，因为输入流中的每个符号在语法分析树中都需要有对应叶节点（事实上，某些分隔符没有）。但对语法中大量使用的部分（如表达式语法），减小渐进时间估算中的常数系数，仍然可以产生足够的差异。

考虑下面的经典表达式语法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

Goal -> Expr
Expr -> Expr + Term
      | Expr - Term
      | Term
Term -> Term * Factor
      | Term / Factor
      | Factor
Factor -> '(' Expr ')'
        | num
        | name

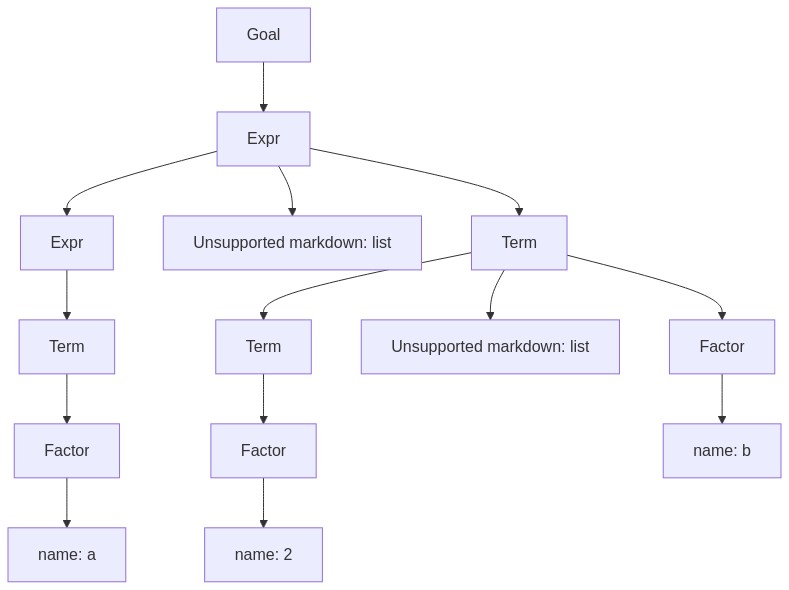
为实施优先级规则，增加了两个非终结符 Term 和 Factor。这样一来，即使对于非常简单的表达式 a + 2 * b，语法分析树也相当大。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

graph TD
A[Goal]-->B[Expr]
B-->C[Expr]
B-->+
B-->D[Term]
C-->E[Term]
E-->F[Factor]
F-->G[name: a]
D-->H[Term]
D-->*
D-->I[Factor]
H-->J[Factor]
J-->K[name: 2]
I-->L[name: b]

任何只有一个子节点的内部节点都是优化的对象。我们通过修改 Term 的规则，至少可以消除一层。

  • 新产生式
1
2
3
4
5
6
7
8
9

Term -> Term * '(' Expr ')'
      | Term * name
      | Term * num
      | Term / '(' Expr ')'
      | Term / name
      | Term / num
      | '(' Expr ')'
      | name
      | num
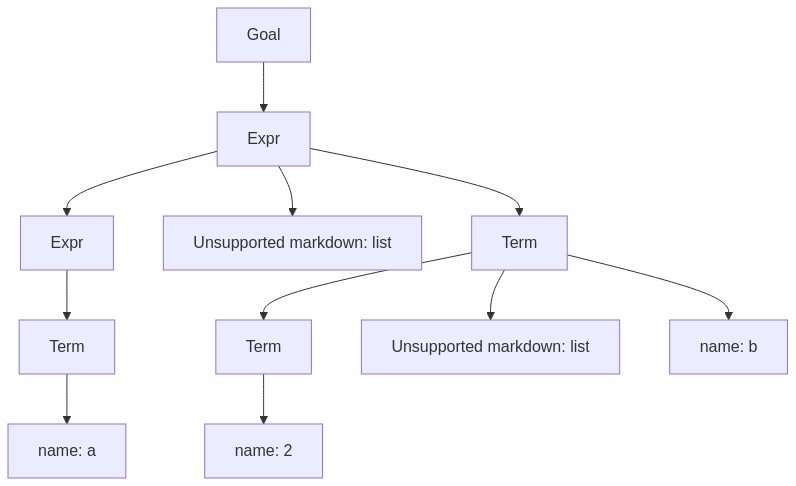
  • 新语法分析树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

graph TD
A[Goal]-->B[Expr]
B-->C[Expr]
B-->+
B-->D[Term]
C-->E[Term]
E-->G[name: a]
D-->H[Term]
D-->*
H-->K[name: 2]
D-->L[name: b]

一般来说，右侧句型只包含任何一个非终结符的产生式，都是可以折叠起来的，这种产生式称为“无用产生式”。

有时，无用产生式有自身的作用：使得语法更紧凑或更具可读性。编译器编写者加入一个无用产生式，可能只是在推导中创建一个点，以便在该点执行某个特定操作。

2. 减小 LR(1) 表的规模

合并行或列

  1. 合并完全相同的行或列
  2. 如果两行/列的不相同之处是其中一列为空白，合并这样的行/列，语法分析对于正确输入仍然会产生正确行为，但改变了错误输入下的行为。

缩减语法

合并终结符：

1
2
3
4
5
6
7

Goal -> Expr
Expr -> Expr addsub Term
      | Term
Term -> Term muldiv Factor
      | Factor
Factor -> '(' Expr ')'
        | val

表的直接编码

放弃表驱动的语法分析器框架，采用硬编码实现：每个状态都变为一个小的 case 语句，或者一组 if-then-else 语句。

由此产生的语法分析器，避免了直接表示 Action 和 Goto 表中的“不关注”表项，但这种对内存空间的节省，可能被增加的代码长度抵消，因为每个状态包含更多的代码。

使用其它构造算法

任何具有 LR(1) 语法的语言，同样有 LALR(1) 语法和 SLR(1) 语法。

规范的 LR(1) 构造法是这些表构造算法中最通用的，它产生的表最大。

参考资料

［1］ Keith D. Cooper. Linda Torczon. 郭旭 译.《编译器设计（第2版）》[M].北京：人民邮电出版社，2020，111-116.